next up previous contents
Next: Casus Irreducibilis Up: Le lezioni Previous: Equazioni risolubili per radicali   Indice

Subsections

L'equazione di terzo grado

Questa parte è presa quasi di peso da [vdW71].

Supponiamo sempre di essere in caratteristica zero.

Discriminante

Denotiamo con $ \Delta(t_{1}, t_{2}, \dots , t_{n}) \in \mathbf{Z}[t_{1}, t_{2}, \dots , t_{n}]$ l'elemento di (7.10.1). Il gruppo simmetrico $ S_{n}$ agisce su $ \mathbf{Z}[t_{1}, t_{2}, \dots , t_{n}]$ permutando gli indici. Un 2-ciclo ha l'effetto di scambiare due colonne della matrice di (7.10.1), e quindi di cambiare il segno di $ \Delta(t_{1}, t_{2}, \dots , t_{n})$. Ne segue che

$\displaystyle \Delta(t_{1}, t_{2}, \dots , t_{n}) \sigma = \begin{cases}\Delta(... ...lta(t_{1}, t_{2}, \dots , t_{n}) & \text{se $\sigma$\ \\lq e dispari,} \end{cases}$ (8.1.1)

Prendiamo adesso un'equazione di grado 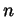$ n$ su un campo $ F$,

$\displaystyle f(x) = x^{n} + x^{n-1} + \dots + a_{1} x + a_{0} = 0,$    

e siano $ \alpha_{1}, \dots, \alpha_{n}$ le sue radici nel campo di spezzamento $ E$. Sia $ G = \Gal ( E / F )$. Allora $ D = \Delta(\alpha_{1}, \dots, \alpha_{n})^{2}$ è fissato da $ G$, e quindi sta in $ F$. $ D$ viene detto discriminante del polinomio o dell'equazione. Per esempio, per l'equazione di secondo grado

$\displaystyle x^{2} + a_{1} x + a_{0} = 0$    

viene proprio il discriminante noto. Infatti

$\displaystyle (\alpha_{1} - \alpha_{2})^{2} = \alpha_{1}^{2} + \alpha_{2}^{2} -... ... (\alpha_{1} + \alpha_{2})^{2} - 4 \alpha_{1} \alpha_{2} = a_{1}^{2} - 4 a_{0}.$    

In generale, dato che $ \Delta(\alpha_{1}, \dots, \alpha_{n})^{2}$ è una funzione simmetrica degli $ \alpha_{i}$, si deve scrivere come un polinomio nelle funzioni simmetriche elementari negli $ \alpha_{i}$, cioè nei coefficienti $ a_{j}$. Sia $ \Omega = \left\{\, \alpha_{1}, \dots, \alpha_{n} \,\right\}$. Abbiamo già notato in 3.3 che la restrizione

$\displaystyle \Gal ( E / F ) \to S_{\Omega}$    

è un morfismo (ben definito e) iniettivo, per cui gli elementi del gruppo di Galois possono essere visti come permutazioni su $ \Omega$, ovvero come elementi di $ S_{n}$.

Lemma 1   Sono equivalenti
  1. Tutti gli elementi di $ \Gal(E/F)$ danno luogo a permutazioni pari.
  2. $ \Delta = \sqrt{D} \in F$.

Dimostrazione. Se tutte le permutazioni sono pari, allora per (8.1.1) $ \Delta = \sqrt{D}$ è fissato da ogni elemento di $ \Gal(E/F)$, e dunque è in $ F$.

Viceversa se $ \Delta \in F$, allora $ \Delta$ è fissato da ogni elemento di $ \Gal(E/F)$, e dunque per (8.1.1) ogni tale elemento rappresenta una pernutazione pari.

Il gruppo di Galois dell'equazione di terzo grado

Veniamo adesso all'equazione di terzo grado

$\displaystyle f(x) = x^{3} + p x + q = 0$    

(le notazioni $ p$ e $ q$ sono tradizionali), a cui supponiamo di aver già rimosso col solito trucco il coefficiente di $ x^{2}$, e prendiamola su un campo $ F$ che contenga una radice terza dell'unità

$\displaystyle \omega = - \frac{1}{2} + \frac{\sqrt{-3}}{2}.$    

Ricordiamo che

$\displaystyle \omega^{2} = - \frac{1}{2} - \frac{\sqrt{-3}}{2}.$    

Tanto vale supporre $ f$ irriducibile su $ F$, altrimenti abbiamo equazioni di grado uno o due, non tre. Dunque il gruppo di Galois $ G = \Gal ( E / F )$ sarà $ S_{3}$ o $ A_{3}$. Infatti sappiamo che il gruppo di Galois è in grado di mandare ciascuna delle tre radici del polinomio irriducibile $ f$ in ciascun'altra, ovvero come gruppo di permutazioni deve essere transitivo sulle tre radici. Che i sottogruppi transitivi di $ S_{3}$ siano solo $ S_{3}$ e $ A_{3}$ è ora facile, dato che gli altri hanno ordine due, e scambiano fra loro due radici, fissando la terza. In ogni caso alla catena di sottogruppi

$\displaystyle G \cap S_{3} \supseteq G \cap A_{3} \supseteq \left\{\, 1 \,\right\}$    

corrispondono i campi fissati

$\displaystyle F \subseteq F(\sqrt {D}) \subseteq E.$    

Quindi la prima estensione radicale è $ F(\sqrt {D}) / F$ (di grado uno o due), e si tratta di esprimere in forma radicale l'estensione di grado tre $ E / F(\sqrt {D})$. Notate che questa è una estensione normale, ed ha gruppo di Galois $ A_{3}$, quindi soddisfa le ipotesi di 7.11.1.

Con alcuni calcoli si può vedere [Jac85] che il discriminante è $ D = - 4 p^{3} - 27 q^{2}$. Siano $ \alpha_{1}, \alpha_{2}, \alpha_{3}$ le tre radici. Formiamo i risolventi di Lagrange

$\displaystyle \left\{ \begin{matrix}(1, \alpha_{1}) &=& \alpha_{1} &+& \alpha_{... ...ha_{1} &+& \omega^{2} \alpha_{2} &+& \omega \alpha_{3}.\\ \end{matrix} \right.$ (8.2.1)

Sappiamo che $ (\omega, \alpha_{1})^{3} \in F(\sqrt {D})$. A questo proposito, vale la pena di notare che il più piccolo campo su cui $ f$ è definito è $ \mathbf{Q}(p, q)$, per cui non si perde niente a supporre $ F = \mathbf{Q}(p, q)$. Dunque $ (\omega, \alpha_{1})^{3}$ deve essere esprimibile in termini di $ p, q, \sqrt{D}$.

Espressione esplicita per le radici cubiche

Per trovare questa espressione in forma esplicita, calcoliamo

\begin{displaymath}\begin{aligned}(\omega, \alpha_{1})^{3} &= \alpha_{1}^{3} + \... ...hantom{=\ } + 6 \alpha_{1} \alpha_{2} \alpha_{3}. \end{aligned}\end{displaymath}

La formula per $ (\omega^{2}, \alpha_{1})^{3}$ è del tutto analoga, dato che basta (ovviamente!) scambiare $ \omega$ e $ \omega^{2}$.

Ora

$\displaystyle \sqrt{D}$ $\displaystyle = (\alpha_{1} - \alpha_{2}) (\alpha_{1} - \alpha_{3}) (\alpha_{2} - \alpha_{3})$    
  $\displaystyle = \alpha_{1}^{2} \alpha_{2} + \alpha_{2}^{2} \alpha_{3} + \alpha_... ...ha_{1} \alpha_{2}^{2} + \alpha_{2} \alpha_{3}^{2} + \alpha_{3} \alpha_{1}^{2}).$    

Se scriviamo temporaneamente

$\displaystyle u = \alpha_{1}^{2} \alpha_{2} + \alpha_{2}^{2} \alpha_{3} + \alph... ...pha_{1} \alpha_{2}^{2} + \alpha_{2} \alpha_{3}^{2} + \alpha_{3} \alpha_{1}^{2},$    

possiamo risolvere il sistema dato dalle ultime due equazioni, ed ottenere

$\displaystyle \left\{ \begin{matrix}\alpha_{1}^{2} \alpha_{2} + \alpha_{2}^{2} ... ...alpha_{3} \alpha_{1}^{2} &=& \frac{1}{2} ( u - \sqrt{D} ). \end{matrix} \right.$    

Ora possiamo riscrivere (8.3.1), tenendo conto che $ \omega + \omega^{2} = -1$ e $ \omega - \omega^{2} = \sqrt {-3}$, come

$\displaystyle (\omega, \alpha_{1})^{3}$ $\displaystyle = \alpha_{1}^{3} + \alpha_{2}^{3} + \alpha_{3}^{3}$    
  $\displaystyle \phantom{=\ } + \frac{3}{2} \omega (u + \sqrt{D}) + \frac{3}{2} \omega ^{2} (u - \sqrt{D})$    
  $\displaystyle \phantom{=\ } + 6 \alpha_{1} \alpha_{2} \alpha_{3}$    
  $\displaystyle = \alpha_{1}^{3} + \alpha_{2}^{3} + \alpha_{3}^{3}$    
  $\displaystyle \phantom{=\ } - \frac{3}{2} u + \frac{3}{2} \sqrt {- 3 D}$    
  $\displaystyle \phantom{=\ } + 6 \alpha_{1} \alpha_{2} \alpha_{3}.$    

Ora vogliamo esprimere

$\displaystyle \alpha_{1}^{3} + \alpha_{2}^{3} + \alpha_{3}^{3} - \frac{3}{2} u + 6 \alpha_{1} \alpha_{2} \alpha_{3}$ (8.3.2)

in termini di $ p = \alpha_{1} \alpha_{2} + \alpha_{1} \alpha_{3} + \alpha_{2} \alpha_{3}$ e $ q = - \alpha_{1} \alpha_{2} \alpha_{3}$: si deve poter fare, perché (8.3.2) è una funzione simmetrica degli $ \alpha_{i}$. Ricordiamo che $ r = \alpha_{1} + \alpha_{2} + \alpha_{3} = 0$. Notiamo

$\displaystyle \begin{matrix}r^{3} &=& \alpha_{1}^{3} + \alpha_{2}^{3} + \alpha_... ... \\ r p &=& && u &+& 3 \alpha_{1} \alpha_{2} \alpha_{3} &=& 0.\\ \end{matrix}$    

Se voglio ottenere un coefficiente $ - 3 / 2$ davanti a $ u$, posso sottrarre dalla prima $ - 9 / 2$ volte la seconda, ottenendo

$\displaystyle 0 = r^{3} - \frac{9}{2} r p = \alpha_{1}^{3} + \alpha_{2}^{3} + \... ...3}^{3} - \frac{3}{2} u + ( 6 - \frac{27}{2} ) \alpha_{1} \alpha_{2} \alpha_{3}.$    

Basta solo aggiungere $ 27/2 \cdot q = - 27/2 \cdot \alpha_{1} \alpha_{2} \alpha_{3}$ per ottenere complessivamente

$\displaystyle - \frac{27}{2} q$ $\displaystyle = \frac{27}{2} \alpha_{1} \alpha_{2} \alpha_{3}$    
  $\displaystyle = r^{3} - \frac{9}{2} r p + \frac{27}{2} \alpha_{1} \alpha_{2} \alpha_{3}$    
  $\displaystyle = \alpha_{1}^{3} + \alpha_{2}^{3} + \alpha_{3}^{3}$    
  $\displaystyle \phantom{=\ } - \frac{3}{2} u + \frac{3}{2} \sqrt {- 3 D}$    
  $\displaystyle \phantom{=\ } + 6 \alpha_{1} \alpha_{2} \alpha_{3}.$    

Quello che abbiamo fatto è un caso particolare di un algoritmo più generale per esprimere una funzione polinomiale simmetrica in termini di funzioni simmetriche elementari: vedi [vdW71].

La morale è che

$\displaystyle (\omega, \alpha_{1})^{3} = - \frac{27}{2} q + \frac{3}{2} \sqrt{- 3 D},$    

e similmente

$\displaystyle (\omega^{2}, \alpha_{1})^{3} = - \frac{27}{2} q - \frac{3}{2} \sqrt{- 3 D}.$    

Prima di estrarre allegramente le radici cubiche, occorre notare che bisogna farlo in modo coerente - una volta scelta la prima, la seconda si determina tenendo presente che

\begin{displaymath}\begin{aligned}(\omega, \alpha_{1}) \cdot (\omega^{2}, \alpha... ...\alpha_{3} + \alpha_{2} \alpha_{3}) \\ &= - 3 p. \end{aligned}\end{displaymath}

Le formule di Cardano

Finalmente possiamo risolvere il sistema (8.2.1), dato che conosciamo i termini di sinistra, e otteniamo

\begin{displaymath}\begin{cases}3 \alpha_{1} = \sqrt[3]{- \frac{27}{2} q + \frac... ...[3]{- \frac{27}{2} q - \frac{3}{2} \sqrt{- 3 D}}\\ \end{cases}\end{displaymath}    

dove una volta scelta una delle tre radici cubiche possibili di $ - \frac{27}{2} q + \frac{3}{2} \sqrt{- 3 D}$, dobbiamo quindi calcolare la radice cubica di $ - \frac{27}{2} q - \frac{3}{2} \sqrt{- 3 D}$ usando (8.3.3).

Esercizio 10 (Facoltativo, ma divertente da provare)   Sia $ F$ un campo di caratteristica diversa da $ 2$ e $ 3$. Si mostri che sono equivalenti le seguenti due affermazioni:
  1. la somma di due quadrati in $ F$ è ancora un quadrato in $ F$;
  2. se un polinomio di terzo grado in $ F[x]$ ha tutte le sue radici in $ F$, allora anche la sua derivata (che sarà un polinomio di secondo grado) ha le sue due radici in $ F[x]$.

next up previous contents
Next: Casus Irreducibilis Up: Le lezioni Previous: Equazioni risolubili per radicali   Indice
A. Caranti
2000-05-31