



Next: Bibliografia
Up: Le lezioni
Previous: Teoria di Galois delle
Indice
Subsections
In questo capitolo vorrei fare due cose:
- La dimostrazione di Cantor dell'esistenza di numeri
trascendenti. Questa si fa semplicemente facendo vedere che i
numeri algebrici sono numerabili, mentre i reali sono più che
numerabili. Lo svantaggio è che non è costruttiva, dato che
alla fine non ci rimane in mano neanche un esempio di numero
trascendente.
- La dimostrazione di Liouville che un numero algebrico non si
può approssimare meglio di tanto con un numero
razionale. Questa ha il vantaggio di pernetterci di costruire
esplicitamente dei numeri trascendenti, ma non ci fornisce nessuna
informazione sulla trascendenza di numeri che a noi potrebbero
interessare.
In un primo momento avevo in mente di fare anche la dimostrazione
della trascendenza di  e
e  , ma poi mi sono reso conto che questa
parte è forse tecnicamente troppo complicata, e alla fine ho
lasciato perdere.
, ma poi mi sono reso conto che questa
parte è forse tecnicamente troppo complicata, e alla fine ho
lasciato perdere.
Un insieme  si dice numerabile quando esiste una mappa
suriettiva
si dice numerabile quando esiste una mappa
suriettiva
 . Se
. Se  è infinito, non sarebbe difficile
vedere che allora esiste una mappa biiettiva di questo tipo. Dunque
è infinito, non sarebbe difficile
vedere che allora esiste una mappa biiettiva di questo tipo. Dunque
 è numerabile se i suoi elementi possono essere messi in una
successione, eventualmente con ripetizioni.
è numerabile se i suoi elementi possono essere messi in una
successione, eventualmente con ripetizioni.
Un insieme finito è naturalmente numerabile, ma
 è ovviamente
numerabile (e infinito), dato che basta prendere l'identità come
mappa
è ovviamente
numerabile (e infinito), dato che basta prendere l'identità come
mappa
 . Anche
. Anche
 è numerabile, come mostra la
successione
è numerabile, come mostra la
successione
Si può considerare questo esempio come un caso molto semplice del
seguente criterio.
Lemma 1 (Zeresimo procedimento diagonale di Cantor)
Sia
 , con ogni
, con ogni  finito. Allora
finito. Allora
 è numerabile.
è numerabile.
Dimostrazione.
Mettiamo gli elementi di ogni

in una successione (finita) a
nostro piacimento. Poi mettiamo tutti gli elementi di

in una
successione, nel modo seguente: prima gli elementi di

,
nell'ordine scelto, poi gli elementi di

, nell'ordine scelto,
e cosí via.
In effetti, si può considerare
 ,
dove
,
dove
 .
.
Esercizio 12 (Primo procedimento diagonale di Cantor)
Si mostri che la tesi del lemma vale anche se si suppone che ogni
 sia numerabile.
sia numerabile.
Ora possiamo vedere che anche l'insieme
 dei numeri razionali è
numerabile. Basta provarlo per i numeri razionali positivi
dei numeri razionali è
numerabile. Basta provarlo per i numeri razionali positivi
 , e poi
applicare lo stesso trucco di
, e poi
applicare lo stesso trucco di
 . Definiamo
. Definiamo
Chiaramente l'unione degli  è tutto
è tutto
 , e ogni
, e ogni  ha
al più
ha
al più  elementi.
elementi.
Consideriamo adesso l'insieme
Anche questo insieme è numerabile. Infatti ogni elemento di  è
radice di un polinomio a coefficienti razionali di grado
è
radice di un polinomio a coefficienti razionali di grado 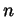 , per
qualche
, per
qualche 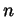 . Se moltiplichiamo uno di questi polinomi per tutti i
denominatori dei coefficienti, otteniamo un polinomio
. Se moltiplichiamo uno di questi polinomi per tutti i
denominatori dei coefficienti, otteniamo un polinomio
ove gli  sono ora interi, e
sono ora interi, e
 . Definiamo
l'altezza
. Definiamo
l'altezza  di tale polinomio come il numero
di tale polinomio come il numero
Di polinomi
![$ f \in \mathbf{Z}[x]$](img1103.gif) di grado
di grado 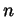 e altezza
e altezza  ce ne sono dunque
al più
ce ne sono dunque
al più
 , e ognuno ha al più
, e ognuno ha al più 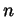 radici. In
particolare è finito ogni insieme
radici. In
particolare è finito ogni insieme
 |
 è radice di un polinomio è radice di un polinomio
![$ f \in \mathbf{Z}[x]$](img1107.gif) |
|
| |
di grado 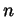 e altezza e altezza  , con , con   |
|
Dato che l'unione degli  è tutto
è tutto  , ne risulta
che
, ne risulta
che  è numerabile.
è numerabile.
Ora resta da vedere che già
 non è numerabile, col secondo
procedimento diagonale di Cantor. Faremo vedere che sono già non
numerabili i numeri reali compresi fra 0 e
non è numerabile, col secondo
procedimento diagonale di Cantor. Faremo vedere che sono già non
numerabili i numeri reali compresi fra 0 e  . Se lo fossero,
potrei scriverli tutti in una successione
. Se lo fossero,
potrei scriverli tutti in una successione
dove  è la
è la  -sima cifra decimale di
-sima cifra decimale di  . Ora le
frazioni che hanno denominatore divisibile solo per i primi
. Ora le
frazioni che hanno denominatore divisibile solo per i primi  e
e  (e quindi danno luogo a uno sviluppo decimale finito)
possono essere scritte in due modi come numeri decimali. Risolviamo
questa ambiguità scegliendo la scrittura infinita, cioè scrivendo
ad esempio
(e quindi danno luogo a uno sviluppo decimale finito)
possono essere scritte in due modi come numeri decimali. Risolviamo
questa ambiguità scegliendo la scrittura infinita, cioè scrivendo
ad esempio
In altre parole, nessun numero nella nostra successione ha tutte le
cifre decimali eguali a zero da un certo punto in poi.
Ora tutto quello che facciamo è di
considerare il numero reale  , compreso fra 0 e
, compreso fra 0 e  cosí
ottenuto. Se
cosí
ottenuto. Se
 , scegliamo
, scegliamo  come
come  -sima cifra decimale
di
-sima cifra decimale
di  . Se invece
. Se invece
 , scegliamo
, scegliamo  come
come  -sima cifra
decimale di
-sima cifra
decimale di  . Viene fuori che
. Viene fuori che  non è nella lista
non è nella lista
 , perché differisce da
, perché differisce da  per l'
per l' -sima cifra
decimale. Ed è comunque scritto nella forma che abbiamo scelto,
perché addirittura non ha alcuno 0 nella scrittura
decimale, per cui certamente non può aver tutti zeri da un certo
punto in poi.
-sima cifra
decimale. Ed è comunque scritto nella forma che abbiamo scelto,
perché addirittura non ha alcuno 0 nella scrittura
decimale, per cui certamente non può aver tutti zeri da un certo
punto in poi.
Sia
 algebrico di grado
algebrico di grado  . In particolare,
. In particolare,
 non è un numero razionale. Scriviamo
non è un numero razionale. Scriviamo
per quello che non è proprio il polinomio minimo di  su
su
 , ma è invece quel polinomio a coefficienti interi che si
ottiene moltiplicando il polinomio minimo per il prodotto dei
denominatori di tutti i coefficienti.
, ma è invece quel polinomio a coefficienti interi che si
ottiene moltiplicando il polinomio minimo per il prodotto dei
denominatori di tutti i coefficienti.
Sia
 , con
, con
 . Calcoliamo
. Calcoliamo
Dunque
Scegliamo  abbastanza vicino a
abbastanza vicino a  , in modo che sia
, in modo che sia
 . Abbiamo dunque
. Abbiamo dunque
e dunque
Ne segue
Ovviamente la costante  non dipende da
non dipende da  . Prendiamo
. Prendiamo  . Otteniamo
. Otteniamo
Ora ovviamente
 , dato che
, dato che  è irriducibile in
è irriducibile in
![$ \mathbf{Q}[x]$](img1134.gif) . Si ha inoltre
. Si ha inoltre
Il numeratore è un intero non nullo, dunque in modulo almeno  . Ne segue
. Ne segue
che vale per  , e per
, e per
 .
.
Vogliamo ricavare un criterio per la trascendenza di un numero.
Proposizione 1
Sia

, con

.
Siano
 interi positivi, tali che
interi positivi, tali che
Allora  è trascendente.
è trascendente.
Dimostrazione.
Facciamo vedere che non esiste il numero

sopra citato. Per
qualsiasi

, fissiamo
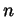
, e scegliamo

tale che

.
Abbiamo quindi
Ne segue che

non può essere algebrico di grado
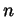
. Dato
che
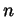
era arbitrario, vuol dire che

è trascendente.
Ora si può fare la costruzione di Liouville, o qualcosa di
simile. Consideriamo la successione
 per per  . . |
|
In altre parole
 .
Definiamo (questo andrebbe spiegato un attimo meglio, anche se
dovrebbe essere corretto)
.
Definiamo (questo andrebbe spiegato un attimo meglio, anche se
dovrebbe essere corretto)
e
Abbiamo quindi
In pratica, il numero  che abbiamo costruito è (controllare)
che abbiamo costruito è (controllare)




Next: Bibliografia
Up: Le lezioni
Previous: Teoria di Galois delle
Indice
A. Caranti
2000-05-31
![]() e
e ![]() , ma poi mi sono reso conto che questa
parte è forse tecnicamente troppo complicata, e alla fine ho
lasciato perdere.
, ma poi mi sono reso conto che questa
parte è forse tecnicamente troppo complicata, e alla fine ho
lasciato perdere.
![]() si dice numerabile quando esiste una mappa
suriettiva
si dice numerabile quando esiste una mappa
suriettiva
![]() . Se
. Se ![]() è infinito, non sarebbe difficile
vedere che allora esiste una mappa biiettiva di questo tipo. Dunque
è infinito, non sarebbe difficile
vedere che allora esiste una mappa biiettiva di questo tipo. Dunque
![]() è numerabile se i suoi elementi possono essere messi in una
successione, eventualmente con ripetizioni.
è numerabile se i suoi elementi possono essere messi in una
successione, eventualmente con ripetizioni.
![]() è ovviamente
numerabile (e infinito), dato che basta prendere l'identità come
mappa
è ovviamente
numerabile (e infinito), dato che basta prendere l'identità come
mappa
![]() . Anche
. Anche
![]() è numerabile, come mostra la
successione
è numerabile, come mostra la
successione
![]() , con ogni
, con ogni ![]() finito. Allora
finito. Allora
![]() è numerabile.
è numerabile.![]() ,
dove
,
dove
![]() .
.
![]() sia numerabile.
sia numerabile. ![]() dei numeri razionali è
numerabile. Basta provarlo per i numeri razionali positivi
dei numeri razionali è
numerabile. Basta provarlo per i numeri razionali positivi
![]() , e poi
applicare lo stesso trucco di
, e poi
applicare lo stesso trucco di
![]() . Definiamo
. Definiamo

![]() non è numerabile, col secondo
procedimento diagonale di Cantor. Faremo vedere che sono già non
numerabili i numeri reali compresi fra 0 e
non è numerabile, col secondo
procedimento diagonale di Cantor. Faremo vedere che sono già non
numerabili i numeri reali compresi fra 0 e ![]() . Se lo fossero,
potrei scriverli tutti in una successione
. Se lo fossero,
potrei scriverli tutti in una successione


![]() algebrico di grado
algebrico di grado ![]() . In particolare,
. In particolare,
![]() non è un numero razionale. Scriviamo
non è un numero razionale. Scriviamo
![]() , con
, con
![]() . Calcoliamo
. Calcoliamo





![]() interi positivi, tali che
interi positivi, tali che
 per ogni
per ogni 
 per ogni
per ogni ![]() è trascendente.
è trascendente.


